Atoms or What the World is Made of
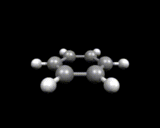 |
What are the ultimate constituents of matter? This question has always fired the scientific imagination; and it remains the intellectual driving force behind one of the largest scale contemporary scientific activities, high energy physics. The Greeks speculated on the nature of the indivisible atoms of matter; and to Newton, atoms were 'massy, hard and impenetrable'. Modern atomic theory was founded by the genius of a Manchester schoolmaster, John Dalton, who suggested that the sparse quantitative chemical data available in the early nineteenth century (mainly concerning the volumes and weights of reacting gases and solids) could be rationalized by postulating that there were different types of atoms corresponding to the different chemical elements; the different atoms had different masses and reacted in simple proportions to give compounds. As the nineteenth century progressed, the concept of the molecule, or aggregate of atoms, took root and, with improvements in the techniques of chemical analysis, the atomic components of key molecules were identified. The idea of molecular shape began to emerge. An important turning point in the science of organic chemistry was the development by Loschmidt and Kekule of the hexagonal ring structure for the molecule benzene, it is this structure that is shown on the left.
Meanwhile, with the identification of an increasing number of chemical elements (i.e. different types of atoms) and determination of their masses, systematic trends in their chemical and physical properties became apparent. The Russian scientist Mendeliev established a tabular classification based on atomic mass, but in which the elements were arranged in horizontal 'periods' each containing eight elements; it was found that the resulting vertical columns or groups of elements in the classification showed significant similarities and trends in their properties. Mendeliev's extraordinarily imaginative classification, which at the time of its formulation necessarily contained gaps and inconsistencies, has subsequently been developed into the modern periodic table of the elements, one of the corner stones of contemporary chemistry.
 |
While chemical knowledge developed rapidly throughout the nineteenth century, the concept of the atom as the ultimate indivisible constituent of matter remained static until, toward the end of the century, a series of startling discoveries began to undermine the foundations of classical physics. In particular, the discovery of the electron - a negatively charged, light sub-atomic particle - by J.J. Thompson and of radioactivity by Becquerel led clearly to the idea of a substructure to atoms. The discovery of X-rays by Röntgen at around the same time also had substantial repercussions to which we will refer later. The next major development was the sensational discovery by Rutherford of the nuclear model of the atom. In one of the greatest scientific experiments of all time, Rutherford's students Geiger and Marsden bombarded a thin gold foil with a beam of α-particles from a radioactive source; the scattered particles were detected by a fluorescent screen. As illustrated schematically below, the results were quite unexpected and extraordinary: whereas the vast majority of the particles went through the foil with only small or negligible deflections, a small proportion were deflected by large angles and a few bounced back! These observations could only be explained by postulating a model in which most of the atom was empty space, with a nucleus with a positive electrical charge and which contained nearly all the mass of the atom. Atoms were already known to be tiny objects (with sizes of the order of a hundred millionth of a centimeter). Rutherford's experiments showed that the size of the nucleus was at least ten thousand times smaller than this. The nuclear model, the basis of all our modern understanding of atomic structure, had been born.
 |
What kind of object is this nuclear atom? The tempting analogy is with the solar system, that is to imagine that the light negatively charged particles (electrons) orbit around the positive nucleus. Such a concept rapidly proved inadequate for several reasons. But before we move toward the modern understanding of the atom, we need to introduce three further concepts which emerged around a hundred years ago. The first is that of quantization. This idea was advanced initially by Max Planck who found that to explain the distribution of frequencies in the electromagnetic radiation emitted by black bodies it was necessary to postulate that energy was not exchanged continuously but in discrete amounts, known as quanta. The idea was further developed by Einstein, who, in the same year that he published his Special Theory of Relativity, showed that to explain the photoelectric effect - the observation that on shining a beam of electromagnetic radiation on solids, electrons were emitted for light above a certain threshold frequency - it was necessary to postulate the energy of the radiation was parceled into discrete lumps or quanta, whose magnitude depended on the frequency of the radiation. These quanta of electromagnetic radiation were named photons. Evidence for quantization of the energies of atoms emerged in the developing science of atomic spectroscopy, which studies the absorption and emission of electromagnetic radiation by atoms. Atomic spectra consist of series of discrete frequencies converging on well defined limits; atoms therefore exchange energy with radiation in a quantized and not a continuous manner. The energies of the atoms are therefore quantized.
A brave attempt was made by Neils Bohr to stretch the 'planetary' model of the atom to include quantization. The orbiting electrons were allowed only certain energies in Bohr's model; and the rules which Bohr proposed explained the spectra observed for the simplest of all atoms, hydrogen, which has one electron circulating around its nucleus. Bohr's model, however, failed for more complex atoms and was quite unable to confront an even more bizarre phenomenon, the wave-like property of matter at the atomic and subatomic level.
The first clear evidence for this strange behavior came from an experiment of Davidson who shone a beam of electrons on to a thin gold foil (just as Rutherford and his students had bombarded gold foil with α-particles). The results were again dramatic: the pattern of the electrons detected behind the foil was in the form of a series of haloes which 'resemble those produced when light is passed through a diffraction grating'. The latter is simply a regular two dimensional structure formed, for example, by drawing lines on glass. Light is a form of wave motion; when it is transmitted through a grating, it shows alternations of intensity depending on whether the radiation transmitted from different parts of the grating is superimposed in or out of phase. In the former case the intensity is enhanced; in the latter, it is reduced. But this is just what was seen in Davidson's experiment with electrons. Moreover, the gold foil might be expected to act like a diffraction grating since, as we shall see, it contains a regular array of atoms. The implications were clear: the electrons behave like waves and are diffracted by a 'grating' provided by the gold atoms in the film. Further evidence for the wave like properties of matter at the atomic level accrued; and it was shown by de Broglie that there was a well defined (inverse) relationship between the wavelength of a particle and its momentum.
The fact that beams of atoms or subatomic particles like electrons can have both particulate and wave-like properties was (and remains) difficult to comprehend; but it is of immense importance (being, for example, at the heart of the modern technique of electron microscopy). It also has strange consequences that undermine some of the fundamental tenets of classical physics. Thus if an electron (or another particle) is behaving like a wave, with a well defined wavelength (and hence, according to de Broglie, a well defined momentum) we have little knowledge as to where it is precisely. If we try to find out where it is, that is to localize it, we change its wavelength and hence its momentum. It turns out that whatever experiments we try to do, we cannot have exact knowledge of a particle's position and momentum simultaneously. This is one formulation of Heisenberg's celebrated uncertainty principle, which represents a radical departure from the strict determinism of classical physics. It is not possible to have a full and precise knowledge simultaneously of all the variables of a microscopic system, and any attempt to gain such knowledge is frustrated by the experiments themselves as these perturb and change the system studied.
Any theory or even description of the atom must take into account these three features of the new physics that emerged early in this century, namely quantization, wave-particle duality and uncertainty. The theoretical physicists of the 1920s were, however, able to rise to this challenge. Heisenberg, Schrödinger Dirac and others formulated a new mechanics - quantum or 'wave' mechanics - appropriate to microscopic objects like atoms. Like classical mechanics (and indeed any scientific theory) quantum mechanics rests on postulates which are stated and cannot be proved; their validity is judged by the success of the resulting theory in rationalizing and predicting observation. Quantum mechanics starts by postulating that we can describe our system by a 'wave function' (often symbolized by the Greek letter Ψ). Ψ depends on the positions of the particles (and in the more general formulation, on time). We must, of course, define the physical interpretation of Ψ. The square of the wave function (Ψ) and not the wave function itself, has physical meaning; and it is interpreted as a 'probability' function. The value of Ψ at a particular point is the probability of finding the particle (or particles) to which Ψ refers at that point; for the hydrogen atom, Ψ will tell us the probability density of the electron at various distances from the nucleus. The 'probabilistic' approach dictated by the uncertainty principle is therefore built into quantum mechanics.
The next step is to formulate an equation that allows us to calculate Ψ. Here the pioneers of quantum mechanics were most ingenious. They were able to take one of the fundamental equations of classical physics, that representing conservation of total energy, and recast it in a form whose solutions are consistent with the requirement of the new mechanics and, of course, with observation. They found that by replacing the momentum in the classical equations by a derivative (or gradient) of Ψ, they could effect the transformation from classical to quantum mechanics. The resulting equations, (the Schrödinger equations), when solved give wave-like solutions. For a free particle (like a free electron) a pure 'sine-wave' solution is obtained; the wavelength depends upon the energy and the momentum in the way postulated by de Broglie. For a confined particle - an electron confined to a box with fixed dimensions or an electron in an atom - as we see, only certain wavelengths and forms are allowed in the solution to the Schrödinger equation; just as when we pluck a violin string or set a hollow cylinder vibrating, only certain waves are allowed. These 'standing wave' solutions correspond to well defined energies; and since only certain solutions are allowed, there are only certain correspondingly well defined energies. Quantization emerges naturally from wave mechanics; the energies of wave-like particles are necessarily quantized when they are confined.
How do we envisage the atom in the light of quantum mechanics? Atoms are positive nuclei which have trapped electrons. The planetary model of orbiting electrons has its conceptual base in classical physics and is inappropriate. The quantum mechanical model is less easy to envisage but it is more elegant and equally intuitive. Around the nucleus we have standing waves of electron density; each solution of the Schrödinger equation corresponds to a different wave form, a different pattern of electron density, with, of course, a different energy. The nearest (but far from exact) analogy is with the standing waves set up in a resonating hollow sphere that too have their different but well defined shapes. This profound and beautiful model of atomic structure is, moreover, in agreement with experiment. When we calculate for the hydrogen atom the energies corresponding to the different solutions of the Schrödinger equation (which are referred to as different orbitals, owing to a lingering affection for classical physics) we obtain values that agree accurately with spectroscopic data.