The Molecular Universe

The electron density of a caffeine molecule.

We have emphasized the unique model building power of contemporary computers. How can we exploit this power to learn about the behavior of atoms and molecules? Two broad strategies are available to contemporary scientists. In the first, we attempt to solve the Schrödinger equation - to learn in detail about the distribution and energies of the electrons in the molecule; and by calculating the energy of the molecule for a variety of geometries, we can try to predict the lowest energy structure. Remember that the Schrödinger equation can be solved exactly only for the hydrogen (and other one electron) atoms. And there exist a whole range of approximate methods for solving the equation for more complex systems. The best of these can now achieve highly accurate descriptions for molecules (and solids) of increasing size and complexity.

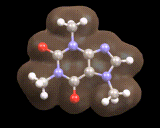
Here we see a molecule produced in nature, caffeine, the image below shows the calculated electron density for the important mineral MgSiO₃. In both cases the computer provides a detailed understanding of the distribution of electrons which govern the molecule's or material's properties.

The electron density in MgSiO₃.

Indeed, calculations on molecules such as caffeine and crystals such as MgSiO₃ are playing an increasingly important role in understanding the behavior of the nature's molecules and the materials from which the earth is constructed.

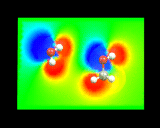
These methods yield an enormous wealth of information. They allow us to understand how electron density is redistributed when atoms form molecules - the process which, as we have seen, is at the very heart of chemical bonding. In addition, from our knowledge of the density of electrons we can calculate the electrostatic potentials around molecules - a crucial quantity which controls the way in which the molecule interacts with other surrounding molecules. The image on the left shows the electrostatic potential on a plane through a water molecule (left) and methanol molecules (right).

The electrostatic potential about H₂O and CH₃OH.

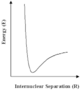
With the continuing growth of computer power, calculations of the distribution of electrons in molecules and hence of molecular structures and properties, will extend to increasingly large and complex molecules and solids. However, even with the largest, most sophisticated computers available today (and in the foreseeable future), such methods will be limited as the amount of computer time and memory increases rapidly with the size of the system studied. But for many of the problems which are posed by highly complex molecules or materials, we can use alternative simpler procedures, based on an old concept in chemistry and physics known as the interatomic potential. We can understand this simple idea by reference to the diagram on the left showing schematically how the energies of a pair of atoms vary with their distance apart (more accurately, their internuclear spacing). When the two atoms are close to each other, their nuclei will repel strongly, as will the 'core' electrons. The energy will therefore begin to increase very rapidly as seen in the diagram. Conversely, when they are a long way apart they will attract each other, due to chemical bonding or the weak 'non-bonding' interactions. The variation of energy with distance will therefore be expected to have a minimum as shown in the diagram.

Interatomic potential schematic. The separation of two atoms is shown on the x axis, the potential energy of the atom pair is plotted on the y axis.

Over the last fifty or so years, scientists have built up detailed information on such interatomic potentials for a wide variety of atom pairs. Moreover, the concept can be extended to larger numbers of atoms. We can learn how the energy of not just two, but three or four or larger numbers of atoms depend on their relative positions (although it may be more difficult to represent these diagramatically). The source of this information is first experiment: the properties of molecules and larger aggregates of atoms depend on the ways in which the atoms interact; and the experimental data may therefore be inverted to yield interatomic potentials. But of course direct calculations of the type described above are, as we have argued, to a growing extent able to give accurate information on the ways in which atoms interact. They are therefore an increasingly reliable source of high quality interatomic potentials.

A data base of good accurate interatomic potentials is a rich repository of information on matter at the atomic level. And the computer is well suited to the processing of this information content into detailed models of the behavior of molecules and materials. A variety of computational approaches may be used. The simplest and most economical (but very powerful) procedure is to exploit a fundamental principle of nature, that is that systems tend to run down hill. We will discuss in more detail the factors which control the direction in which systems evolve. But if we want to predict the structure of a molecule or a solid, it is normally a valid procedure to search for the lowest energy arrangement of atoms.

This simple approach - often referred to as energy minimization (or molecular mechanics when used specifically for molecules) is illustrated diagramatically on the left. We must, of course, start by guessing a structure for our molecule - the starting point, S, and we will consider later how these points are defined. But once the initial configuration of atoms has been defined, the procedure is simple. The atoms are systematically moved around in such away that the molecule is driven 'down hill' in energy. In practice, this 'minimization' proceeds by a succession of moves or 'iterations', each of which involves a small displacement of some or all the atoms; the energy of the system is calculated from the data base of potentials, as are normally the forces on each atom which guide the direction and magnitudes of the atomic displacements. The calculation ends when a minimum is located; that is a point is reached (like M on the left) which represents the lowest energy, and any displacement from this point will raise the energy.

This simple but powerful method can work remarkably well. On the left we show trajectories of in the first case a simple peptide and in the other a crystal structure that have been successfully energy minimized. In both cases, the minimized structure is an accurate model of reality; and in each the 'starting point' is remote from the final minimum.

Energy minimization and its effect on the conformation of a peptide molecule.

Adjusting the calculated structure of a benzene crystal structure to match a powder diffraction pattern.

Energy minimization is now a standard tool of the computational chemist. But the technique is, however, limited. There are fundamental limitations arising from the whole basis of the concept: the energy minimum is often a good guide to the structure of a molecule or crystal; but the science of thermodynamics tells us that other factors must be considered in a detailed theory of the stability of matter at the atomic level. A second (and related) limitation arises from the use of purely 'static' models. No account is taken of the fact that atoms are in constant motion; and the dynamical behavior of molecules influence their structures and stabilities. Then there may be serious practical limitations, of which possibly the most important is illustrated in above in the energy surface schematic. Here we illustrate the course of a minimization which starts from 'S' and ends at the point 'ML'. This is indeed a minimum, but it is not the lowest one; for if we run 'up hill' a little and pass over barrier B, we will move down into the lower minimum, 'M'. The minimum 'ML' is known as a 'local minimum'. And calculations starting from any point in the valley around this minimum will end up at this point. In complicated molecules (like those in biological systems) or solids, there may be many hundreds of local minima, and the task of finding the lowest energy or 'global' minimum becomes increasingly difficult. many different starting points must be sampled, and even then there is no guarantee that the global minimum will have been located. Minimization, therefore, although widely used by the computational scientist, is often only the first stage of a computational study of matter at the atomic level.

The next level of sophistication remedies one of the major deficiencies of minimization calculations. It represents the dynamic nature of matter at the atomic level.

The conceptual basis of the molecular dynamics technique is again simple. In the system to be simulated - for example, the molecules, cluster of molecules or crystal - we assign all atoms not just positions but velocities; and the latter are chosen with a target temperature in mind. We then allow the system to evolve in time subject to the forces acting on all the atoms (which can be calculated using the interatomic potentials). Normally, 'classical' mechanics is used; that is, the equations of motion first formulated by Newton are applied to the dynamics of atoms. This classical approach works surprisingly well for all but the lightest of atoms; and more sophisticated 'quantum' methods are available when, for example, the dynamics of hydrogen atoms are modeled.

Let us look, however, in a little more detail at the way in which simulations work. In many ways they work like a movie: they consist of a succession of snapshots closely spaced (in time) which when run together create a representation of continuous motion, as shown schematically on the left, where we consider four atoms: each has a position and a velocity at the 'first frame'.

Schematic illustration showing molecular dynamics time steps.

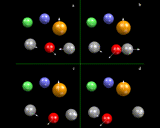We now allow time to move forward a small amount (Δt) to the second frame. Since we know how fast the atoms are moving, it is straightforward to work out their new positions in the new frame; they will simply have moved by their velocity times Δdt. But we also know the forces acting on the atoms, which we can work out from our knowledge of the interatomic potentials. And if we know the force, Newton's celebrated Second Law of motion tells us we can work out accelerations - that is the extent to which the velocities are changing with time - so we can calculate the new velocities in the new frame. We then move onto the next frame and the next; and in a real simulation tens, if not hundreds, of thousands of frames will be used in creating a dynamical record of the system.

The choice of the time step (Δt) is, of course, crucial. If it is too long, it will give a simulation which is like an old style 'jumpy' movie. And indeed the criterion for the choice of 'time step' (Δt) is very similar to that used in choosing the time lapse between frames in movies. It must be short compared with the time of any important process in the system: in movies this may be the time to kick a ball or to pull and fire a gun. In the molecular world, it is the time taken by a molecule to vibrate or rotate. The time taken to kick a ball is roughly a second or so; and the time between frames in movies is a hundredth to a thousandth of a second. Molecules have different time scales: they vibrate and rotate in periods of a million millionths (10^-12) seconds. The time steps must be a hundred or a thousand times smaller than this (i.e. 10^-15 seconds). So if we collect a million time frames (roughly the limit of current calculations), we can watch how our simulated system evolves in a thousand millionths (10^-9) seconds. But a lot can happen in molecules and materials during this period!

We show three typical dynamics trajectories below: the first relating to the biological molecule oxytocin. The second shows the trajectories of ions moving in a solid electrolyte at high temperatures. The migrating ions carry electric charge and hence this material is a good conductor of electricity - a fact which has stimulated interest in its use in advanced batteries. Finally we show an animation of successive frames from a simulation of water which shows that the position of water molecules rapidly change in liquid water.

A molecular dynamics trajectory calculated for the hormone oxytocin.

A molecular dynamics trajectory showing the tracks of lithium ions in a conducting polymer.

Snapshots from a simulation of liquid water. One of the molecules is shown in yellow to highlight its trajectory through the course of the simulation.

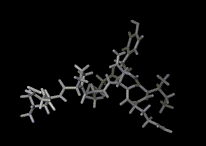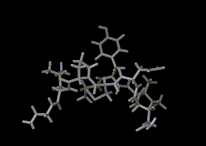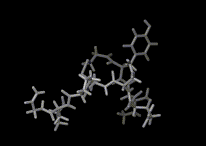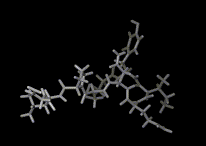Molecular dynamics has proved to be an enormously productive technique for the computational chemist, physicist and biochemist. The method has been applied to an extraordinary variety of systems - proteins, pharmaceuticals, industrial polymers, complex crystals, solids, glassy materials and a huge range of liquids. Simulations using this method yield a rich range of information on both structures and dynamics of the system simulated. Indeed, molecular dynamics has often been referred to as a 'molecular microscope' which yields details on the behavior of matter at the atomic level which are inaccessible from experiment. Again, however, the method is limited. We have already discussed the time scale of the simulations - at most 10^-9 seconds even with the biggest, most powerful modern computers. So the processes we are interested in must take place within this time. And although this is long on the molecular time scale, important events may often not be sampled in this period. Two typical examples relate firstly to the 'relaxation' and reorientation processes in polymers, which exert a crucial influence on the dynamics of these systems and which may have time scales in the range 10^-12 to 10¹ seconds; and secondly to diffusion in solids (which although in some cases relatively fast as shown on the left) is normally slow, taking place by infrequent 'hops' of atoms between different sites in the solid. For the size of system simulated (which is discussed in greater detail below) few, if any, such jumps will take place over the time scale of a molecular dynamics simulation. So phenomena like corrosion, which depend on slow diffusion processes in solids, cannot be usefully investigated by this technique; although it turns out that simpler methods, akin to the energy minimization approach, but in which we chart the change in energy of a migrating atom as it moves between two sites, are effective for probing atomic dynamics in these systems.

A related but distinct point concerns the size of the simulated system. The simplest of statistical considerations suggests that the larger the number of atoms in the simulation, the greater will be the probability of observing events (such as the hops of atoms between sites as discussed above). Modern simulations are performed typically on thousands of atoms (although calculations on millions of atoms are becoming increasingly common). In simulating solids, which extend indefinitely in three dimensions, an ingenious strategy is used. The group of atoms being simulated (often referred to as the simulation box or cell) is surrounded by images of itself that extend to infinity as illustrated schematically (in two dimensions) on the left. A finite group of particles can therefore be made to represent an infinite system. In the case of crystals periodicity that this procedure imposes - the content of all the boxes are identical - may correspond to reality since, as we will see, the defining feature of crystals at the atomic level is that the arrangement of atoms is periodic. For liquids and glasses this periodicity is artificial; but the procedure is nevertheless useful.

Other computational methods will be discussed at appropriate points later on. We hope, however, that the discussion above has shown how the computer is a uniquely powerful tool in constructing models for matter at the atomic level. The horizons of the field of computational studies of matter have expanded rapidly in the last ten years. Developments in both hardware and software have played their role in this spectacular growth of the subject.

We have concentrated on the model building power of computers at the microscopic level. Their unique capabilities are also being exploited to model engineering, global and cosmic systems. We can extend our understanding of matter at the atomic level by exploring the properties and behavior of gigantic numbers of atoms and molecules.