Computers, Molecules, and Materials
|
In the 1950s, the distinguished theoretical chemist, Professor Charles Coulson, attempted, together with a colleague, Dr. Bill Moffatt, to undertake a calculation on the nitrogen molecule [1] - a simple species, comprising two light atoms which we know are very strongly bound. Coulson was studying the most fundamental problem in chemistry, the question of why atoms form molecules. The calculation he performed aimed to investigate the bonding characteristics of the molecule - the distribution of electrons around the nuclei and the energy levels of the electrons in the field of the nuclei. It used developments of the quantum mechanical theory describing the distribution of the electrons in atoms that had been formulated by Schrödinger in the 1920s. The technology available to Coulson was a mechanical hand calculator. After several months work, the study was abandoned as it was estimated that it would take another 20 years to complete, which was sufficient to daunt even such a dedicated scientist as Coulson.
Using a modest computer, of the type that is routinely available today, it is possible to perform a calculation on the nitrogen molecule of a much more sophisticated type than that which Coulson attempted. Within a few seconds - a far shorter time that it takes to describe Coulson's frustrating failure - we are able to calculate the energy of the molecule, and the results of the calculation allow us to map out the distribution of electrons and to determine their energy levels which is, of course, the basis of the understanding of the chemical bond in this molecule. We can look at individual orbitals - individual energy levels - for electrons. For example, it is the basic topological features of the highest occupied orbital in this molecule which control many of its properties. Such calculations when undertaken on modern computers require just seconds. Coulson's calculation (which employed sweeping approximations) can be performed in thousandths of a second. It is in fact a very simple, trivial and routine application of modern computational technology to a basic problem in the study of chemical bonding. Moreover the impact of this technology on chemistry is indicated, not only by the transformation of a twenty-year calculation into a millisecond calculation, but also by the fact that state-of- the-art calculations are studying molecules of considerable complexity, for example, the decapeptide derivative of the immuno-suppressive drug cyclosporin [2] which contains 63 carbon as well as 11 nitrogen and 12 oxygen atoms which we will return to later.
![(The decapeptide derivative of the drug molecule cyclosporin studied using ab initio quantum mechanical methods by Price et al [2].)](http://www.themolecularuniverse.com/MMMGIF/cyclosporin_l_scale.gif)
|
Indeed, this article aims to show that this type of technology is having a profound impact on science, first, by allowing us to understand in detail the way in which atoms interact to form molecules - by amplifying our knowledge of chemical bonding, and as we have seen, by allowing us to study molecules of much greater complexity that the simple N2 molecule; secondly, by enabling us to understand - and increasingly to predict - the manner in which atoms in complex molecules and solids arrange themselves - for example, in biological molecules such as lysozyme whose structure was first determined at the Royal Institution; and in the beautiful porous inorganic crystal structure known as zeolites which play a major role in the petrochemicals industry and whose structures and properties are currently being intensively studied by both computational and experimental methods at the Royal Institution and many laboratories around the world. Thirdly, we will see how computational methods reveal beautifully the motion, the dynamics of matter at the atomic level.
We will see that computational techniques are applicable across a wide range of modern science - chemistry, physics, biology and materials and earth sciences; moreover, that they can contribute to important areas of applied science and technology - for example, the behavior of fission products that accumulate in the fuels of nuclear reactors as they burn up, or the design of new pharmaceuticals.
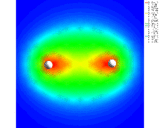
Our first theme concerns the understanding of the chemical bond, of the ways in which atoms interact with each other and the prediction of the properties of the resulting molecules which has been the central preoccupation of the theoretical chemist during the last 60 years. We know that atoms form bonds because when atoms come together their electron density is redistributed so as to reduce the energy of the system. We also know that this redistribution can take place in three distinct ways. In the first (covalence), which is illustrated by the simple example of the hydrogen molecule, the electrons are concentrated between the nuclei where their potential energy is low due to their exposure to the strong electrostatic field of both nuclei. Computationally based calculations reveal directly the enhancement of electron density as shown by the results of the calculations on the hydrogen molecule which is displayed as a contour map on the left. The piling up of density between the nuclei is clearly seen. This is the basis of the bonding in a wide range of molecules and solids; for example, in silicon, the important semi-conducting material, the atoms are held together in the solid by just this type of density enhancement.
|
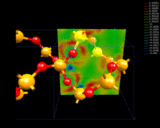
Our second mode of electron density redistribution (ionic bonding) involves transfer of electrons between atoms with lower to higher affinities for electrons. Let us consider the example of quartz, SiO2 - important both as a mineral and as an industrial material. The structure was first determined by Bragg [3] and comprises SiO4 linked together by sharing their corners. During the last year, Roberto Nada - a student at the Royal Institution - has used computational techniques to look in great detail at the way electron density is distributed around the Si and O atoms in this crystal [4]. These results, shown on the left, reveal very clearly the transfer of electrons from the Si to the O atoms which is the basis of the chemical bonding in this system. The detailed nature of the electron density distribution shown by these calculations is complex; it has some of the elements of covalence (i.e. concentration) in addition to ionicity. The essential point is that we can map out in detail the complex distribution of electrons in this solid. We can look, for example, at what happens to the material at very high pressures when the 4-fold coordination of the Si changes to a coordination of 6 oxygen atoms to give the mineral stishovite found in rocks that have been subjected to very high temperatures, and pressures as in meteoritic impact. The bonding now shows a higher degree of electron density transfer - a prediction which we hope will be verified experimentally.
|
Computational methods also reveal beautifully the basis of the third type of electron redistribution - the converse of the first - that is delocalisation or spreading out of the electrons which lowers their kinetic energy. To illustrate this we take a molecule that has played a central role in the development of theoretical organic chemistry - that is benzene - the cyclic molecule comprising of six carbon and six hydrogen atoms, which was discovered in 1825 by Michael Faraday in the Royal Institution. Faraday isolated benzene by distillation from oil gas that in turn was produced from whale oil. His interest in this oil had been first stimulated by his involvement in a court case concerning a fire in a sugar refinery where he had appeared as an expert witness, the question being the relative flammability of sugar and oil. It is interesting to note that in this court case Davy and Faraday appeared as witnesses for the opposite sides of the cause!
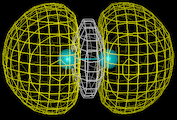
Benzene shows a high degree of stability, which we now know can be related to the fact that some of the electrons in the molecule are in delocalized rings of electron density above and below the plane of the molecule - a result that is shown directly by computational techniques and which can be illustrated by modern molecular graphics as illustrated on the left, which represents the topology of one of the delocalized orbitals in this molecule.
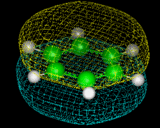
|
So far we have shown how the methods of computational chemistry can clothe the simple framework of chemical bonding theory. The field is, however, entering a very exciting sphere when, owing largely to the rapid expansion in the computer power, these types of calculations can be preformed on much more complex molecules. For example, Martyn Guest and co-workers at the SERC Daresbury Laboratory have, as noted above, investigated the important peptide derivative of the drug, cyclosporin. Their calculations, which have determined the distribution of electron density throughout this highly complex molecule, allow us to study in detail the accessible surface of the molecule, which enables us to predict how this molecule interacts with other species and also to gauge the accuracy of more approximate ways of modeling the molecule which will be discussed shortly. Another example is provided by work in progress by Roberto Dovesi and co-workers at the University of Turin who are carrying out electronic structure of calculations on sodalite - a zeolite (albeit a relative simple one) with the aim of probing the electric field within the cage.
Interatomic Potentials and Energy Minimisation
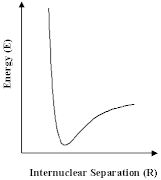
The developments described above are most important. Nevertheless, the scope of such calculations is limited. For very large molecules that biologists are interested in, or materials such as many of the zeolites which are so important to the industrial chemist, it is not possible to solve the Schrödinger equation at an acceptable level of approximation. Nor is it, for many of the questions that we are asking about those systems, desirable or necessary. We can have recourse to other approaches, which will give the information that we most want more directly and simply. The methods that we will now discuss in most of the remainder of this article are all based on an old idea, that of the ineratomic potential in which we simply express the energy of a group of atoms as depending on the relative positions of their nuclei. In the simplest case we have a pair atoms, for which the variation of energy with internuclear distance is shown schematically; but we can use the same approach for larger numbers of atoms.
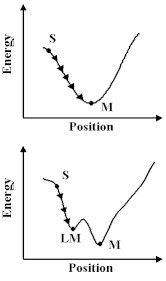
How do we learn about these potentials? Firstly, we can study the properties of molecules and solids - their structures, the way in which they vibrate and their compressional properties - and deduce the potentials; or secondly, we can calculate them using the methods we discussed earlier. Let us assume, however, that we have built up a `library' of the relevant potentials for the molecule and material that we are studying, then there are a number of interesting things we can do. First, we can exploit a universal principle of nature, that is things run down hill. So what we have to do is move our atoms to lower the energy, however, this is a non-trivial exercise; we have to undertake the procedure as a succession of steps or `iterations'. And if we relied on a hand calculator we would, like Coulson, soon abandon the attempt in all but the simplest system. Computers are, however, excellent at repetitive operations; so we can use them very effectively to carry out these calculations. But before we do so, we should note that there is a difficulty. The computer can allow a molecule or a crystal to run down-hill, as shown; but we cannot be sure that it has found at the bottom of the lowest energy valley. So we can run down hill to the nearest local minimum; but we do not know that there is not another one lurking somewhere else. With this caveat in mind, let us see this method in action.
|
|
Peptides, Proteins and Pharmaceuticals
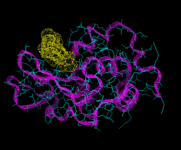
We will consider first biological molecules. In particular we will look at the field of peptide and protein structure. These are chain molecules. The sequence of organic groups derived from the parent amino acids (of which there are 20 distinct types and which vary from simple species such as H and CH3 to more complex aromatic groups) defines the molecule. Peptides are relatively short chains containing less than approximately 50 or so residues; and proteins are longer structures. These molecules do not however, normally occur as extended chains; their chains wrap and fold around themselves to give a much more compact structure, as in the enzyme lysozyme shown on the left. Moreover, the functioning of the protein is determined by its tertiary (3D) structure. On of the greatest challenges of contemporary science is to understand and ultimately predict the nature of protein folding. In the early days of energy minimization calculations, it seemed that this method might hold the key. These hopes have not been realized for reasons which we will refer to shortly; but let us first see a successful application of the method to a relatively simple peptide, apamin, which is isolated from bee venom.
|
Apamin is an 18-residue peptide containing S-S bridges; it is of interest and importance because it is a potent neurotoxin. Its amino acid sequence is shown on the left. We will consider minimization of the energy of this biological molecule, starting from an extended configuration; minimization is of course, to a considerable extent driven by the need to shorten the -S-S-bond. The image on the left shows four configurations in the minimization sequence starting from and extended structure with the stretched -S-S-bond and ending with a compact energy minimum. It turns out there is a lower energy structure than that shown in the fourth image. This is also shown on the left and represents what we now consider to be the global energy minimum of this peptide; it has a high content of a-helical structure and was generated by energy minimization calculations [5].
Of course, this is a simple calculation which omits the effects of water by which the peptide is always surrounded. But there is good evidence that the conformation is approximately correct.
A far more complex example is provided by the important human renin enzyme which has recently [6] been refined by energy minimization calculations. This study indicates the complexity of system that can be handled by contemporary energy minimization methods.

|
Let us now look at a different but closely related set of applications in the area of pharmaceutical design. First we note that many biological processes work by one type of molecule binding to a specific site in a second type of molecule (the receptor) and that many drugs work by the drug molecule blocking the receptor by itself docking in and binding to the receptor thereby inhibiting its action. Energy methods of the type we have been discussing are widely used now in industry to simulate this process and guide the design of new drugs.
We can provide a simple illustration by considering the enzyme dihydrofolate reductase which plays an important role in DNA synthesis. If we can find molecules which obstruct this activity we can suppress DNA synthesis in the cell leading to cell death. It would be of particular benefit if we could obtains pharmaceuticals which bind to the bacterial form of the enzyme rather than the vertebrate forms. Such an example is provided by the molecule trimethoprim which we can dock into the active site of the E-coli version of the enzyme [7]. Such methods have an established track record in assisting the design and optimization of new pharmaceuticals.
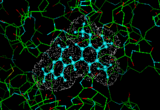
|
Despite these successes, it is important to stress that energy methods of the type we have described have serious limitations. The first is the local minimum problem to which we have already referred. This difficulty is particularly severe with large biological molecules such as proteins which may have many thousands of local minima; and for this reason the methods are, in practice, often only used to refine approximately known structures. A second and in many ways and even more fundamental limitation is that entropic effects are ignored. The second law of thermodynamics tells us that systems evolve to their lowest `free energies' rather than energies; and the free energy can be equated to the energy only if the entropy is negligible - a condition that is unlikely to be realized in flexible polymeric molecules such as proteins. Thirdly, in the earlier applications of the methods, the effects of solvating water molecules, by which biological molecules are generally surrounded, were ignored. It is now clear that the effects of solvent can be profound; and they are being included increasingly in modern calculations. Finally, it has become clear that even at room temperature, biological molecules are highly mobile and dynamic. Such effects are necessarily omitted from simple energy calculations, but can be included in `dynamical' simulations as discussed later in this article. These inadequacies should always be borne in mind when using straightforward energy minimization calculations which, however, continue to have a wide range of applications.
Crystals and Defects
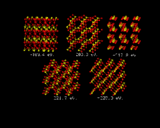
Let us now turn our attention to the inorganic world, in particular the field of inorganic crystal structures, where the application of computational methods is in many ways more straightforward and where the potential pay-off is equally great. We will look first at using the computer to predict crystal structures. The ultimate goal here would be to specify the chemical composition of a crystal and use knowledge of interatomic potentials to predict their structures. Progress in this endeavor is being made by a number of groups around the world. We will give one illustration of recent work done at the Royal Institution. It concerns a relatively simple inorganic structure titanium dioxide. What we have done here is to generate a random configuration of Ti and O atoms within the unit cell - the basic repeat of the crystal - and let the system run down hill. It does so into the rutile structure, which is the stable polymorph of TiO2, as is shown in the sequence of configurations on the left. The initial configuration illustrates the initial arrangement of atoms generated by the computer; the subsequent images represent stages in the energy minimization; the lattice energies which are given with each configuration become progressively more negative. At the end of the sequence the system has `crystallized' into the rutile structure [8].
We should emphasize that this approach of throwing atoms into the unit cell at random is not going to work in general, and will probably fail in most materials with highly complex structures. Nevertheless, this simple demonstration for TiO2 is encouraging. For general purpose structure refinement packages, what we need are approximate rules to guide our choice of starting point. Such rules would use empirical knowledge of crystal structures of related compounds in order to generate a number of possible `starting points' for energy minimizations. Given such an approach there is now a chance of real progress in this area and it may, moreover, be possible to develop new computational methods that will be able to predict new structures.

|
Let us continue by exploring the role which computation can play in the study of zeolitic materials referred to earlier. The materials are aluminosilicates built up of SiO4 and AlO4 tetrahedra sharing corners, as shown on the left. Because we are replacing Si by Al, the framework is negatively charged. The negative charge may be neutralized by adding protons to the bridging oxygens which confers very acidity on these materials. Alternatively, we can incorporate positive ions, such as Na+, K+, and Ca2+ in the pores of the zeolite. These ions can be readily exchanged, leading to one of the most important properties of zeolites - ion exchange. Indeed, zeolites have been used for many years as water softeners, with more recent high-technology applications being the removal of radioactive ions from the contaminated water after the Three Mile Island and Chernobyl nuclear accidents [9].
But it is on their acidity that we shall concentrate, as this makes the materials potent catalysts. Organic molecules can diffuse into the zeolite and undergo a variety of reactions, with the nature of the reaction being controlled by the geometry by the zeolite pore - the phenomenon of shape selective catalysis. Common zeolite structures are shown on the left. The porous nature of the crystal architecture is clearly revealed. Several structures are based on the sodalite unit shown which may be linked by sharing four rings to yield the structure zeolite-A which is widely used in the detergent industry of its ion exchange properties or by sharing six rings resulting in the zeolite-Y structure which contains a large void, known as the supercage. Large hydrocarbon molecules can be accommodated in such voids, where they undergo acid catalyze cracking reactions to smaller hydrocarbons, in the gasoline range. The zeolite ZSM-5, shown on the left, is based on a different type of network comprising ten and five rings and has the converse type of catalytic application in that it can be used for synthesis of hydrocarbons from methanol.
The understanding of zeolite catalysis, requires us to be model, first the location of molecules within the zeolite and secondly, how they react. We will look at one illustration: methanol (CH3OH) in ZSM-5 which , as we have noted, catalytically converts the molecule into hydrocarbons in the gasoline range. Energy minimization methods can be used to locate the site occupied by the sorbed molecule, as shown on the left. We can then use electronic structure methods to see how the molecule reacts at the site into which it has docked. We can illustrate this with the work of Julian Gale [10] at the Royal Institution whose calculations show how the docked molecule is partially protonated by the OH group of the framework - the first stage in the catalytic reaction.
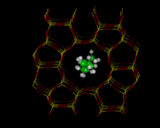
|
We can of course locate far more complex molecules than methanol, for example, the early work of John Thomas and Tony Cheetham locating pyridine in zeolite L [11] and the recent work of James Titiloye and Stephen Parker [12] has shown how octane is accommodated within the pores of ZSM-5 and how it modifies its conformation, how it wriggles into the pore structure of this zeolite as shown on the left.
Before we leave energy calculations, we must mention a class of calculation that has had a very substantial impact on several areas of solid state physics and chemistry. It concerns the behavior of impurities and defects in solids which it is known often control many of their most important properties. It rests on a simple idea advanced by Neville Mott over 50 years ago [13], by which was then developed computationally at Harwell in pioneering work in the 1970s [14]. The basis of the method is illustrated on the left. A region (containing typically 100-300 atoms around the defect) is relaxed to equilibrium; the response of more distant regions can be adequately described by approximate methods.
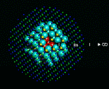
|
We will give two illustrations of the use of these methods. The first concerns nuclear fuels - uranium dioxide which is used in most modern nuclear reactors - the particular problem being the behavior of the fission products created within the fuel as it burns up. The process of fission produces a wide range of elements. Fission products may be volatile or soluble in the fuel if they are able to form oxide or metallic precipitates.
We will focus on one particular product, Xe - a rare gas - that is highly insoluble in UO2 and whose behavior influences the properties of the fuel very considerably. It is most important to know where this atom is situated in the UO2 matrix. Calculations, initially in the 1970s [15], but refined more recently by Robert Jackson and Robin Grimes [16], show how the atom digs itself into a hole by ejecting U and O atoms to create a `tri-vacancy' (a complex of one uranium and two oxygen vacancies). Moreover, Robin Grimes' work has now led to very detailed predictions of the location of most of the fission products.
Our second application concerns high temperature superconductivity - probably the most important development in solid state science in the 1980s. Superconductivity - the ability of materials to conduct electricity without resistance - is most important technologically and has been of fundamental interest to physicists for many years. The phenomenon is only observed at low temperatures; and until 1987, after decades of research, the highest temperature at which superconductivity had been observed had been ~20K in complex alloy systems. Then in a remarkable breakthrough Bednorz and Muller [17] showed that an oxide material - La2CuO4 - was superconducting up to ~40K, and subsequent discoveries [18] found that more complex oxide materials could attain superconducting transition temperatures of >90K - that is, above liquid nitrogen temperature, which offers the opportunity of an enormous expansion in superconducting technology.

|
The crucial issue in superconductivity concerns the interaction between charge carriers; in particular, can charge carriers, in this case the oxidized species, couple to form pairs. Calculations undertaken recently at the Royal Institution by Xiaozhong Zhang [19] have suggested, interestingly, that the superconducting oxide materials are particularly effective at screening the repulsive interactions between pairs of charge carriers. Indeed, in some cases there is a net attraction.
We should stress that this is not a theory of superconductivity in these materials. It is more a suggestion of why these oxides might provide the right kind of matrix for the pairing of charge carriers, which is the basis of superconductivity.
Dynamics
![(Successive configurations in the simulation of the melting of SiO<sub>2</sub> showing melt formation from the crystalline to the liquid state. Results taken from reference [20].)](http://www.themolecularuniverse.com/MMMGIF/sio2_melting_scale.gif)
|
So far, everything we have considered has concerned static assemblies of atoms. But matter at the atomic level is dynamic - atoms are in constant motion - and their motion is beautifully revealed by a third type of computational method. The technique of molecular dynamics (MD) that we now describe is based on a simple idea. A `simulation box' is set up containing particles that represent the atoms in the system simulated. Each particle is given a position and a velocity, the latter being chosen with a target temperature in mind. The system is then allowed to evolve in time by specifying a `time-step' dt, which must be shorter that the period of any characteristic process (E.g. a molecular vibration period) in the system; typically dt is 10-15 to 10-14 seconds. The classical equations of motion are used to update the positions and velocities for this change in time; forces acting on each particle are calculated from knowledge of the interatomic potentials, and Newton's second law of motion enables the resulting changes in velocity to be calculated. The process is repeated several thousands times to allow us to build up a picture of the time evolution of the system. Indeed an MD simulation contains a full dynamical record of the system simulated within the limitation of a classical description and albeit for a limited time span (typically 10-1000 ps; 1ps =10-12 s). But within this period - a few million millionths of a second, plenty can happen at the atomic level!
The first application that we will describe concerns melting and glass formation. Molecular dynamics can simulate melting, i.e. the conversion of a relatively static, crystalline array of atoms into disordered and mobile assembly of atoms, as illustrated on the left. We can then use the computer to quench, i.e. withdraw heat from the melt and generate a frozen disordered configuration, which provides a good way of simulating the structures of glasses, which are, indeed, traditionally made by quenching from the melt. A computer generated structure [20] for vitreous (glassy) silica (SiO2) is shown on the left.

|
|
Our next example concerns the behavior of the lower part of the Earth's mantle which the recent work of David Price and Alison Wall [21] has shown may be an enormous solid electrolyte. Their simulation shows that in this dense high temperature mantle mineral, oxygen ions can readily migrate and the conductivity they calculate is compatible with the estimate of the mantle conductivity - a result which has major implications for our understanding of the electromagnetic behavior of the earth.
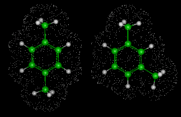
Next we will look at the zeolite systems we considered earlier and show how dynamical properties are crucial in these materials. The particular example we take concerns the behavior of two isomers of xylene - meta (m) and para (p) - whose structures are illustrated on the left. Conversion of m into p xylene is an industrially important process, which can be successfully catalyzed by the zeolite ZSM-5. This acidic catalyst readily allows CH3 groups to flip between the m and p positions. Production of the desired p product (which is subsequently used in the synthesis of polymeric materials) is promoted by the greater diffusivity of the p isomer, which can therefore escape more readily from the zeolite. The higher diffusion coefficient of p xylene is directly demonstrated by simulation studies that illustrate motion of the isomers in ZSM-5.
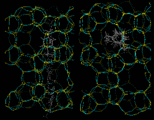
|
|
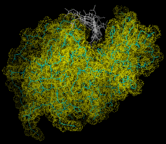
Finally we consider the dynamics of biological molecules. These are best revealed diagrammatically. Thus the image on the left shows a succession of configurations for lysozyme, generated by a MD simulation, that have been superimposed. The large amplitudes of motion of the side groups are particular apparent.
The ability to simulate the detailed behavior of biological molecules is a good illustration of the power and scope of modern computational techniques. We should, however, emphasize that it is not the aim of computational techniques to simply mimic nature, although predictive applications of the methods are very valuable. The most important applications of these methods are to reveal the contrasting state of order and disorder, but above all the intricacy and beauty of matter at the atomic level.
References
1. The information on Coulson and Moffatt's calculation was
provided by Dr W.G. Richards to whom we are grateful.
2. Price, S.L., Harrison, R.J., and Guest, M.S. 1989, J. Comp.
Chem., 10, 552
3. Bragg, W.H. and Gibbs, R.E. 1925. Proc. Roy. Soc., A, 109,
405
4. Nada, R., Catlow, C.R.A., Dovesi, R. and Pisani, C., 1990.
Phys. Chem. Minerals, 17, 353
5. Freeman, C.M., Catlow, C.R.A., Hemmings, A.M. and Hider,
R.C. 1986. FEBS Lett., 197, 289
6. Hemmings, A.M., Foundling, S.I., Sabanda, B.L., Wood, S.P.,
Pearl, L.H. and Blundell, T.L. 1985. Biochem. Soc. Trans, 13,
1036
7. Dauber-Osguthorpe, P. et al. 1988. Proteins, 4, 31
8. Freeman, C.M. and Catlow, C.R.A. J. Chem. Soc. Chem. Comm.,
1992. 89-91
9. King, L.J., Campbell, D.O., Collins E.D., Knauer, J.B. and
Wallace, R.M. 1984. In: Olson, D. and Bisio, A. (eds),
Proceedings of the Sixth International Zeolite Conference, p.
660, Butterworths
10. Gale, J.D., Catlow, C.R.A. and Cheetham, A.K., 1991. J.
Chem. Soc. Chem. Comm. 178
11. Wright, PA., Thomas, J.M., Cheetham, A.K. and Nowak, A.K.
1985, Nature, 318, 611
12. Parker, S.C., Titiloye, J. and Catlow, C.R.A. 1991, J.
Phys. Chem. 95, 1991
13. Mott, N.F. and Littleton, M.J. 1938 Trans. Faraday Soc.,
34, 485
14. Norget, M.J., 1974. UKAEA Report, AERE-R7650
15. Catlow, C.R.A., 1978. Proc. Roy. Soc. London A, 364, 473
16. Grimes, R. and Catlow, C.R.A. 1991. Phil Trans. Roy. Soc.
London 335, 609
17. Bednorz, J.G. and Muller, K.A. 1988. Z. Phys. B., 64, 189
18. Wu, M.K. et al. 1987. Phys. Rev. Lett., 58, 908
19. Zhang, X. and Catlow, C.R.A. 1991, J. Chem. Soc. Materials
Chemistry, 1, 233
20. Vessal, B., Amini, M., Fincham, D. and Catlow, C.R.A.
1989. Phil Mag. 60, 753
21. Wall, A. and Price G.D. 1988. Am Miner., 73, 224